A constante de Planck e os níveis de energia no átomo de Bohr
Este material é parte integrante do Jogo do Prêmio Nobel de Atomística
© Carlos Alberto dos Santos, Eliabe Maxsuel de Aquino, Farnésio Vieira Diniz
© Carlos Alberto dos Santos, Eliabe Maxsuel de Aquino, Farnésio Vieira Diniz
Na página anterior, vimos que cada nível, n, no átomo de hidrogênio está associado a uma energia dada pela fórmula
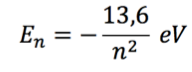
Nossa questão agora é entender a constante 13,6.
Essa constante é facilmente obtida a partir dos postulados de Bohr, mas alguns dos conceitos de física envolvidos são do conhecimento de poucos alunos do ensino médio. Para nosso objetivo aqui é suficiente saber que ela depende da carga e da massa do elétron, da constante dielétrica no vácuo e da constante de Planck, h.
Essa constante foi introduzida em 1900, por Max Planck (1858-1947), quando ele apresentou a primeira hipótese da quantização da energia, segundo a qual, no nível atômico a energia não pode ter qualquer valor. Só existe energia com valores proporcionais a essa constante. Essa hipótese marca o nascimento da teoria quântica. Os valores dessa constante nos três principais sistemas de unidade são:
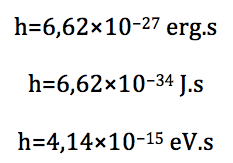
Entre seus postulados, Bohr afirmou que as energias do elétron nas órbitas atômicas eram tais que a passagem de um nível para outro só podia envolver energias que satisfizessem a relação
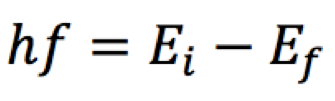
Ou seja,
- se o nível i é mais próximo do núcleo que o f, então o elétron terá que receber energia de uma radiação eletromagnética com frequência, f, tal que seu produto com a constante de Planck seja igual à diferença das energias.
- por outro lado, se o nível i é mais afastado do núcleo que o f, então o elétron emitirá uma radiação eletromagnética com frequência, f.
Vamos agora usar esta fórmula para explicar as séries espectrais do hidrogênio, observadas no final do século 19, mais de uma década antes de Bohr apresentar seus resultados.
Voltar para a Biblioteca